La rupture diopienne : colloque du Caire. 1974

L'apport de l'Afrique à la civilisation universelle, Conférence de Niamey, 1984 - vidéo

Jean-Philippe Omotundé : les mathématiques africaines, Afrique, berceau de l'écriture - vidéos

Vidéo : Jean-Marc Bonnet-Bidaud : Visions africaines du ciel

Audio : JP Omotundé : l'héritage scientifique de l'Afrique antique dans le domaine des mathématiques.

Kossivi ADJAMAGBO - Cheikh M'Backé DIOP :  Papyrus Rhind et le Papyrus de Moscou + la tombe de SENENMUT - Sitographie

Théophile Obenga : la tutelle intellectuelle doit cesser - vidéo

A black history of the world : http://realhistoryww.com/

***

Le Colloque du Caire, 1974

Le peuplement de l'Egypte ancienne et le déchiffrement de l'écriture méroïtique

http://www.ankhonline.com/revue/colloque_egyptologie_caire_1974.htm

le Colloque d'égyptologie du Caire en 1974 - Cheikh Anta Diop

https://www.yumpu.com/fr/document/view/16571326/le-colloque-degyptologie-du-caire-en-1974-cheikh-anta-diop/7

***

Cheikh Anta Diop

L'apport de l'Afrique à la civilisation universelle

30. 4. 2016

30 ans après sa disparition, le nom et l'oeuvre de ce grand savant restent encore méconnus.

Des forces s'ingéniant à contrôler les discours, s'emploient à maintenir l'enseignement de Cheikh Anta Diop dans le néant de la page blanche.

On peut observer dans cette analyse...

http://www.jerome.estranky.cz/clanky/wwi/cheick-anta-diop.html

...leur fonctionnement pour la langue tchèque dans le système de communication en ligne.

Pour les Francophones, s'ils désirent découvrir la nouvelle fabuleuse histoire racontée par Cheik Anta Diop, la tâche est plus aisée...cependant, les élus se cantonnent encore à quelques happy few (la vidéo étant très longue...)

La conférence de Niamey (1984)

Mise en ligne le 27 avr. 2011 par Nzwamba

https://www.youtube.com/watch?v=TzIEn60nGbU

http://www.cheikhantadiop.net/cheikh_anta_diop_apport_afrique_civilisation.pdf

***

30e anniversaire de la disparition de Cheick Anta DIOP

Publié le vendredi 29 juillet 2016

A l’occasion du 30e anniversaire de la disparition du savant sénégalais Cheick ANTA DIOP, une conférence-débat a été organisée le mercredi 27 juillet 2016 à l’Institut français d’Abidjan. Une initiative du Club des lecteurs dudit institut.

Sous la modération du Pr Ramsès BOA TIEMELE, enseignant-chercheur de Philosophie à l’Université Félix Houphouët-Boigny, le Dr Cissé Chikouna, historien et enseignant-chercheur d’Histoire dans la même Université, s’est livré à l’exercice consistant à revisiter la vie et l’œuvre de l’intellectuel sénégalais dont la pensée et l’œuvre marquent une rupture dans l’historiographie africaine. Il s’est agi pour le Dr Cissé Chikouna, qui revendique l’héritage intellectuel du chantre du panafricanisme, de présenter l’homme, de faire revivre les points saillants de son œuvre et d’en évoquer la postérité.

Le conférencier, dans cette perspective, a d’abord rappelé la formation intellectuelle de l’homme ; laquelle formation reste dominée par les mathématiques et la philosophie. Sa rencontre pédagogique avec le philosophe Gaston Bachelard, note-t-il, le stimule à œuvrer pour la rupture épistémologique dans la conception de l’histoire africaine. Physicien nucléaire, Cheick Anta DIOP est d’abord traité comme un paria intellectuel, d’autant plus que le jury commis à la soutenance de sa thèse portant sur l’avenir de la pensée africaine, ne rencontre aucune adhésion. Il la publie cependant, par la suite, sous l’intitulé ‘’Nation nègre et culture’’.

Le postulat de Cheick Anta Diop qui sera confirmé par la suite, poursuit l’orateur, c’est de démontrer que l’Egypte pharaonique est de civilisation négro-africaine.

Prônant une Conscience historique forte des Africains, socle de leur indépendance culturelle, politique et économique de ce continent ayant subi l’esclavage et la colonisation, deux violents chocs historiques.

Le fondateur du laboratoire de datation au carbone 14 voyageant beaucoup et animant des conférences de grandes envolées scientifiques fut contacté en 1966 par l’UNESCO dans le cadre d’un projet de réécriture de l’histoire générale de l’Afrique. C’est alors que Cheick Anta DIOP propose un grand débat scientifique mondial sur l’histoire de l’Afrique, en particulier le caractère négro-africain de la civilisation de l’Egypte pharaonique. ‘’DIOP sort auréolé de ce débat et l’UNESCO décide de publier l’histoire de l’Afrique en tenant compte des observations de DIOP’’, note le conférencier. Qui n’a pas manqué de souligner que ce grand intellectuel africain a été marginalisé dans son pays le Sénégal et n’a pas connu le succès politique escompté.

Le Dr Cissé CHIKOUNA a du reste relevé la dimension œcuménique de la pensée de Diop, montrant son caractère universaliste. Pour finir, l’orateur a indiqué que le savant africain n’a pas pu transmettre l’héritage aux nouvelles générations mais il appartient à cette postérité de s’approprier ledit héritage en vue de la Renaissance Africaine.

http://news.abidjan.net/h/595400.html

***

JP Omotundé :

Les mathématiques africaines

Emission de radio Sankofa - 14 avril 2016 mise en ligne par UhemMesut

Afrique, berceau de l'écriture

Mise en ligne le 10 févr. 2012 par Chaîne de IshangoTV

"Visions africaines du ciel" par Jean Marc Bonnet Bidaud

***

JP OMOTUNDE : l'héritage scientifique de l'Afrique antique dans le domaine des mathématiques.

Le 1er décembre, dans l'émission "Hier et ailleurs", NK Omotunde était interviewé par Eric Lefevre dans le cadre de la Fête des Sciences 2017, sur l'héritage scientifique de l'Afrique antique dans le domaine des mathématiques.

***

Sur la mesure du cercle et de la sphère en Égypte ancienne

Kossivi ADJAMAGBO - Cheikh M'Backé DIOP

Résumé : Dans le présent article sont commentés deux problèmes mathématiques traités dans deux papyrus égyptiens : le calcul de l'aire d'un cercle (Papyrus Rhind) et le calcul de la surface d'une demi-sphère (Papyrus de Moscou). Ces calculs constituent la première formulation connue, dans l'histoire universelle des mathématiques, des problèmes suivants : la quadrature du cercle, la rectification de la circonférence et l'aplanissement d'une surface courbe. Nous montrons l'importance du rôle joué par la notion de mesure dans l'établissement des formules égyptiennes. L'examen des formules mathématiques égyptiennes révèle à la fois une démarche théorique implicite et la mise au point de techniques algorithmiques et numériques efficientes pour résoudre des problèmes concrets.

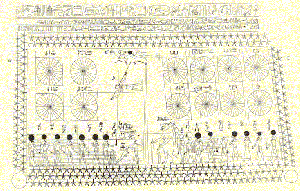
Plafond astronomique de la tombe de SENENMUT (vers 1500 av. J.C.). SENENMUT était l'architecte du temple de la reine HATSHEPSUT (Deir el Bahari). On note la discrétisation des cercles en 24 secteurs égaux.

Conclusion

Tirant toutes les conséquences des faits mathématiques égyptiens se rapportant au calcul de la surface du cercle et de celle de la demi-sphère respectivement exposés dans le Papyrus Rhind et le Papyrus de Moscou nous avons abouti aux conclusions suivantes :

— la propriété du rapport constant entre la surface d'un cercle et son diamètre est connue des Égyptiens et il s'agit d'une problématique distincte de celle de la quadrature qui vise à déterminer l'équivalent égyptien du facteur p pour approximer la surface d'un cercle par celle d'un carré.

— l'étude conjointe des problèmes relatifs au calcul de la surface du cercle et de la surface d'une demi-sphère montre que les relations internes entre les caractéristiques d'un cercle sont connues des Égyptiens.

— Les formules de calcul de la surface du cercle et de la demi-sphère, telles qu'elles apparaissent — c'est-à-dire générales et exactes — dans le Papyrus Rhind et le Papyrus de Moscou, supposent l'introduction de la notion de mesure au sens mathématique du mot que le mathématicien Égyptien a su rendre opératoire.

Plus généralement, les papyrus mathématiques égyptiens, et en particulier le Papyrus Rhind, dont le titre est : "Méthode correcte d'investigation dans la nature pour connaître tout ce qui existe, chaque mystère, tous les secrets" [T. OBENGA, La Géométrie égyptienne, op. cit., p. 290], témoignent de cette conquête de la raison humaine : l'homme découvre qu'il peut accéder à la connaissance du réel grâce à des formules mathématiques. Les formes idéales que sont le cercle, le rectangle, le carré, l'ellipse, la pyramide, etc., n'existent nullement dans la nature. L'Égyptien a su concevoir ces formes idéales, reconnaître les propriétés géométriques qui leur sont intrinsèquement attachées, indépendamment de leurs dimensions, traduire ces propriétés en termes de formules mathématiques. L'Égyptien, dans un retour vers le réel, utilise les propriétés ainsi reconnues et les formules mathématiques associées pour résoudre des problèmes concrets : architecture, économie, agriculture, astronomie, etc. A cette fin, le mathématicien met au point des algorithmes de calculs et des conventions numériques qui suffisent à ses exigences de précision.

La découverte de la possibilité de connaître la Nature au moyen d'une formulation mathématique constitue un événement majeur dans l'histoire de la pensée scientifique. En Afrique, cette découverte semble s'être faite au travers de la géométrie, c'est-à-dire de la mesure de la terre étymologiquement parlant, en raison de la configuration géo-climatique particulière de la vallée du Nil, en Égypte même. Les Égyptiens ont puissamment contribuer à ouvrir la voie de la connaissance scientifique du réel, celle qu'ont empruntée à leur suite les Grecs, celle que continue d'emprunter le chercheur d'aujourd'hui.

http://www.ankhonline.com/revue/adjamagbo_pa_cercle_sphere.htm

***

Bio / Des textes on-line :

ANYJART.COM

Culture et Savoir de Nos Ancêtres

***

Théophile Obenga : La Tutelle intellectuelle doit cesser chez les Africains

Ajoutée le 6 nov. 2016 AFRIQUE ou A FRIC?

***

A black history of the world 

http://realhistoryww.com/

***

Les premiers résidants

***

Dernière mise à jour : 24/04/2022